今天咱们来聊聊啥叫“纳什均衡”,听起来这词有点高大上,但其实说白了,就是一种大家都不想换策略的局面。就是说,咱们都在博弈,大家的策略已经都选好了,谁也不想再改,这就是所谓的“均衡”了。
你看嘞,博弈论这个东西,原本是用来研究大家在竞争中怎么作决策的。简单来说,就是当两个人或者多个人有个共同的利益,大家各自做的决策互相影响,最终就有了博弈。而这个纳什均衡呢,就是每个人都选择了一个对自己最有利的策略,结果,哪怕别人改变了自己的策略,也不会让自己得到更多好处。大家都选择了一个最合适自己的路,谁也不想再改变了。
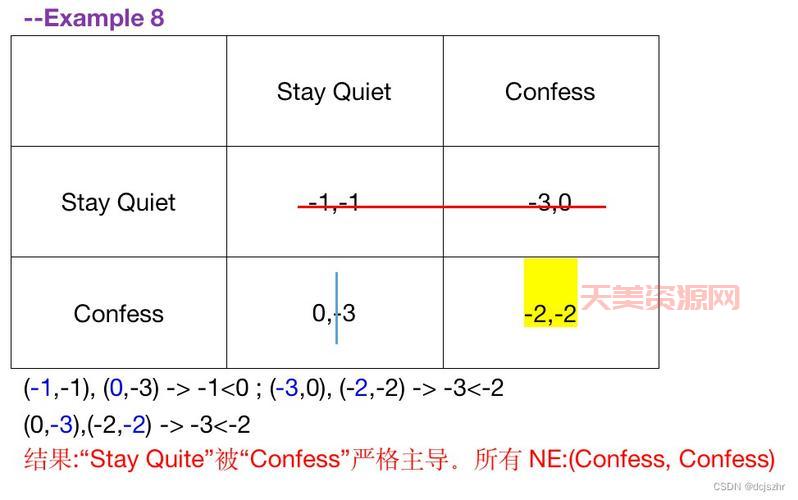
拿两个商家举个例子:假如咱们有两个小商店卖鸡蛋,一个卖的是十块钱一斤,另一个卖的是十二块钱一斤。如果两个商家都定十块钱一斤,那他们俩都能卖出去鸡蛋,也都能赚钱。但是要是其中一个商家把价格降到八块钱一斤,想多卖点,那他可能会卖得更多,但另一个商家也得跟着降价,这样,两个商家都赚得少了。最好的情况是,他们俩都不改价格,这就是纳什均衡。各自守住了自己的最优策略,谁都没得更好的办法。
再说说纳什均衡的由来:这个理论可不是咱们现在才有的东西,早在1950年,约翰·纳什这个人就提出了这个概念。他发现,在不完全信息的博弈里,大家都根据自己知道的信息去选择最合适的策略,然后没谁愿意单独改变了。就像咱们做生意一样,如果大家都在同一条线下竞争,那谁也不敢轻易改变策略,否则就可能赔了夫人又折兵。
有时候你想嘞,咱们都知道纳什均衡的好处,就是稳定,但其实这个均衡也不一定是最优的。例如,在一些寡头垄断的市场里,大家都在博弈,按照纳什均衡的原则,每个人都选了自己最好的策略,但其实如果大家都联合起来制定一个更合理的规则,可能大家都能赚得更多。不过,纳什均衡的好处就是,没人会单独改变自己的策略,维持了局面的稳定。
这种均衡也有点复杂:有些时候,可能会有多个纳什均衡存在。就像是你和别人一起下棋一样,可能有好几个不同的方式让你们俩都不愿意改变自己的策略,这样的局面叫做“多重均衡”。在这种情况下,大家的选择就可能有很多种,而不同的选择又可能影响最终的结果。
说到这,你可能想问了:那怎么知道自己处在纳什均衡中呢?咱们可以通过一个叫做“支付矩阵”的东西来计算。这个支付矩阵就像是一张表格,表格里列出了每个人在不同情况下的收益。如果每个人根据别人的策略来选择最优的策略,最后的结果就是纳什均衡。
举个简单的例子:假设有两个人在卖蛋糕,一个卖十块钱一个,另一个卖十二块钱一个。如果第一个人知道,第二个人定价十二块,他自己就定十块,这样他能卖出去更多,结果就能赚得更多。第二个人如果知道第一个人定十块,他自己就定八块,争取更多顾客。但两人最终会发现,最好的策略就是都定十块钱,这样他们都能稳稳当当地卖出去蛋糕。

这就是纳什均衡的魅力,大家都找到了一个最合适自己的策略,谁也不想单独改动,局面就稳定了。
不过,纳什均衡也有它的局限:有些情况下,大家选择的策略未必是最理想的。在一些复杂的博弈中,可能会有多个均衡,甚至有些均衡看起来大家都不喜欢,但却是最稳妥的选择。这就像你们在开集市,大家都知道有很多摊位,但都选择去那个已经非常热门的位置,即便大家都知道那里早晚会满员,大家却宁愿挤在一起,免得错失机会。
总结一下:纳什均衡呢,其实就是大家都不愿意单独改变自己策略的一个状态,不管别人的策略怎么变,自己都找到了最合适的路。它能带来博弈中的稳定,但并不总是最优解。尽管如此,它依然是一个十分重要的理论,尤其在经济学、政治学等领域里,纳什均衡帮助人们理解了在复杂决策中如何找到一个稳定的局面。
Tags:[纳什均衡,博弈论,策略,经济学,决策,稳定,市场博弈]
